同余基本理论

整除：若整数 bb 除以整数 aa 的商为整数，且余数为 00，则称 aa 整除 bb，记作 a∣ba\mid b > 同余：给定一个整数 mm，若 mm 除整数 aa，bb 的余数相等，就称 aa 与 bb 对模 mm 同余，记作 a≡b(modm)a\equiv b\pmod m

下面证明一个 a≡b(modm)a\equiv b\pmod m 的充要条件

a≡b(modm)a\equiv b\pmod m 的充要条件为 m∣(a−b)m\mid (a-b)

设 a=q1m+r1a=q_1m+r_1，b=q2m+r2b=q_2m+r_2，0⩽r1,r2<m0\leqslant r_1,r_2<m

若 a≡b(modm)a\equiv b\pmod m，则 r1=r2r_1=r_2，故 a−b=(q1−q2)ma-b=(q_1-q_2)m，也即有 m∣(a−b)m\mid (a-b)

若 m∣(a−b)m\mid (a-b)，则可设 a−b=km(k∈Z)a-b=km\quad(k\in\Z)，即 (q1−q2)m+r1−r2=km(q_1-q_2)m+r_1-r_2=km，则 r1=r2r_1=r_2，即 a≡b(modm)a\equiv b\pmod m

从钟表引入

假设钟表显示现在是 1010 点，如果我们想让指针指向 66，我们有两种调法

  • 要么让指针往回拨 44 个刻度，即 10−4=610-4=6
  • 要么将指针往前拨 88 个刻度，即 10+8=18→610+8=18\to 6

为什么要考虑余数？

在十二小时制中，设 nn 表示 nn 时，那么

  • 若 0⩽n⩽120\leqslant n\leqslant12 时，可以直接得到当前的时间就是 nn 时
  • 若 12<n⩽2412<n\leqslant 24，想获取其在十二小时制中对应的时间，我们会用 nn 减去 1212，
  • 若 24<n⩽3624<n\leqslant 36，我们则会用 nn 减去 2×122\times 12

由此可以看出，无论 nn 为多少，想获取其在十二小时制对应的时间，则会用 nn 减去若干倍的 1212，这其实就是一个用 nn 模 1212 取余的过程（注意这里的若干倍可以表明我们并不关注商是多少）

在上面钟表的例子中，我们想让指针指向 66，采用减法的思想是我们比较容易想到的，因为这样可以直接计算 10−4=610-4=6，而如果我们一定要采用第二种方法呢

为什么减44和加88等效？

上面我们讨论到，我们只需要关注余数，也就是说，我们只需要关注 10−410-4 和 10+810+8 的余数

一旦注意到这点，我们就不难想到这样一个同余式

(10−4)≡(10+8)(mod12)(10-4)\equiv(10+8)\pmod{12}

在这里，我们称 88 是 −4-4 在模 1212 系统下的补（不难注意到 44 也是 −8-8 在模 1212 系统下的补）

因此，在模 mm 的系统下，对于任意的 KK，只要满足 AA 与 BB 互补，则有 (K+A)≡(K+B)(modm)(K+A)\equiv(K+B)\pmod m

如何找到对应的补数？

在上面的模 1212 系统中，我们很容易找到 −4-4 的补数，甚至其他数的补数

那么，在任意的一个模 mm 的系统中，如何快速的找到一个数的补数呢，还是回到下面这个式子

(K+A)≡(K+B)(modm)(K+A)\equiv(K+B)\pmod m

根据前文介绍的定理，这个同余式要成立，当且仅当 m∣[(K+A)−(K+B)]m\mid [(K+A)-(K+B)] 成立，也就是

m∣(A−B)m\mid (A-B)

写成等式的形式，即 A−B=km(k∈Z)A-B=km\quad(k\in\Z)，也就是 A=km+BA=km+B，可以看出 AA 的补数可以有无数多个，这里我们取 k=1k=1，那么

A=m+BA=m+B

为了符号的统一，我们令 A,B>0A, B>0，且 AA 就是我们要的 −B-B 的补数，那么就得到了

A=m−BA=m-B

这样，我们就能很容易得到 −4-4 的补数就是 12−4=812-4=8

补码的数学原理

在开始补码之前，我们首先要知道为什么计算机需要补码

以八位二进制数为例，我们依次将最低位到最高位记作第 00 位，第 11 位，第 22 位，…，第 77 位

一般来说，第 77 位是符号位，且正数第 77 位为 00，负数的第 77 位为 11，如

(3)10=(00000011)2(3)_{10}=(00000011)_2，(−5)10=(10000101)2(-5)_{10}=(10000101)_2

我们把这种二进制表示法称为数的原码，记作

[3]原=00000011[3]_{\text{原}}=00000011，[−5]原=10000101[-5]_{\text{原}}=10000101

接下来我们用原码来计算 3−53-5，首先我们要知道的是，计算机并不能处理减法，因此这里实际的运算是 3+(−5)3+(-5)，如下

00000011+1000010110001000\begin{array}{r} 00000011\\ + 10000101\\ \hline 10001000 \end{array}

然而 1000100010001000 对应的十进制数是 −8-8，而非正确结果 −2-2

经过尝试，原码只有在计算正数与正数的和时才能完全正确，因此就有了补码

一个 nn 位的二进制数其实是一个模 2n2^n 的系统

我们先考虑正数，去掉一个符号位，一个正数还有七位，因此八位二进制数能表达的最大的正数是 27−1=1272^{7}-1=127

那么，从 0000000000000000 开始， 如果将这个数不断加 11，就得到 0111111101111111（即 127127），继续加 11，直至 1111111111111111，这时再加 11，就得到了 100000000100000000，而这是一个八位的二进制整数，因此这个数实际上应该表示为 0000000000000000，也就回到了 00

就像时钟一样，从 11 开始走过 1212 格后，又回到了 11，因此（十二小时制）时间就是一个模 1212 的系统

同样的，一个 nn 位的二进制数，可以看成是一个模 2n2^n 的系统

如何定义补码？

在前文中，我们了解到并可以知道非负数的算术运算都是没有问题的

接下来设想一个正数加上一个负数，由前文可知，在模 2n2^n 的系统中，加上一个负数 −a-a，就相当于加上该负数的补，即 2n−a2^n - a，我们将这个数定义为负数的补码

如何计算负数的补码？

定义一个十进制整数 xx 的原码（以八位为例）为 a7a6a5a4a3a2a1a0(ai=0,1,i=0,1,2⋯ ,7)a_7a_6a_5a_4a_3a_2a_1a_0\quad(a_i=0, 1,i=0, 1, 2\cdots, 7)

依据前文定义，正数的补码就是它本身，也即当 x⩾0x\geqslant 0 时，[x]补=a7a6a5a4a3a2a1a0[x]_{\text{补}}=a_7a_6a_5a_4a_3a_2a_1a_0

接下来我们考虑负整数，即当 x<0x<0 时，[x]补=2n−x=[(28−1)−x]+1[x]_{\text{补}}=2^n-x=[(2^8-1)-x]+1，我们将 2n−12^n-1 和 xx 都写成二进制的形式，并做差可得

11111111−a7a6a5a4a3a2a1a0aˉ7aˉ6aˉ5aˉ4aˉ3aˉ2aˉ1aˉ0\begin{array}{cccccccccc} & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ - & a_7 & a_6 & a_5 & a_4 & a_3 & a_2 & a_1 & a_0 \\ \hline & \bar{a}_7 & \bar{a}_6 & \bar{a}_5 & \bar{a}_4 & \bar{a}_3 & \bar{a}_2 & \bar{a}_1 & \bar{a}_0 \end{array}

注意这里 1−ai=aˉi1-a_i=\bar{a}_i 无非就两种情况，列举即可得到这个等式成立

由此，我们便得到了负数的补码在二进制数下的计算公式

[x]补=[x]反+1[x]_{\text{补}}=[x]_{\text{反}}+1

数据溢出

为了方便，接下来我们以四位二进制整数为例

根据前面的知识，四位二进制表示的整数的范围为 [−8,7][-8, 7]，将这些整数和对应的补码表示在数轴上如下

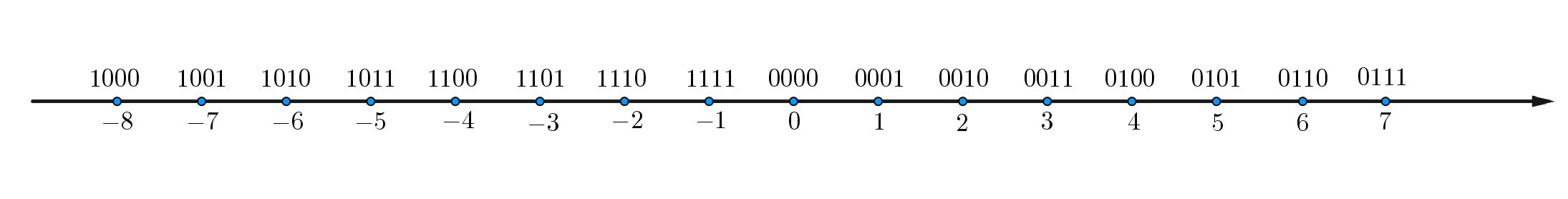
我们发现 7+17+1 本应对应 88，然而由于 0111+0001=10000111+0001=1000，而使得结果为 −8-8，虽然不符合常理，但是这样就限制了所有的数的范围都在 [−8,7][-8, 7] 这个区间内，同时，我们把 7+1=−87+1=-8 这种情况称为溢出，特殊地，这是一个上溢出（88 比最大值 77 大）

同样地，7+27+2 也不会等于 99，而是等于 −7-7，换成数数的算法，我们可以知道 77 的后一位是 −8-8，77 的后两位是 −7-7，以此类推得到 77 的后 99 位回到了 00

那么，我们不妨将这些数放在一个圆上（将数轴绕成一个圆），就可以得到下面的这种表示

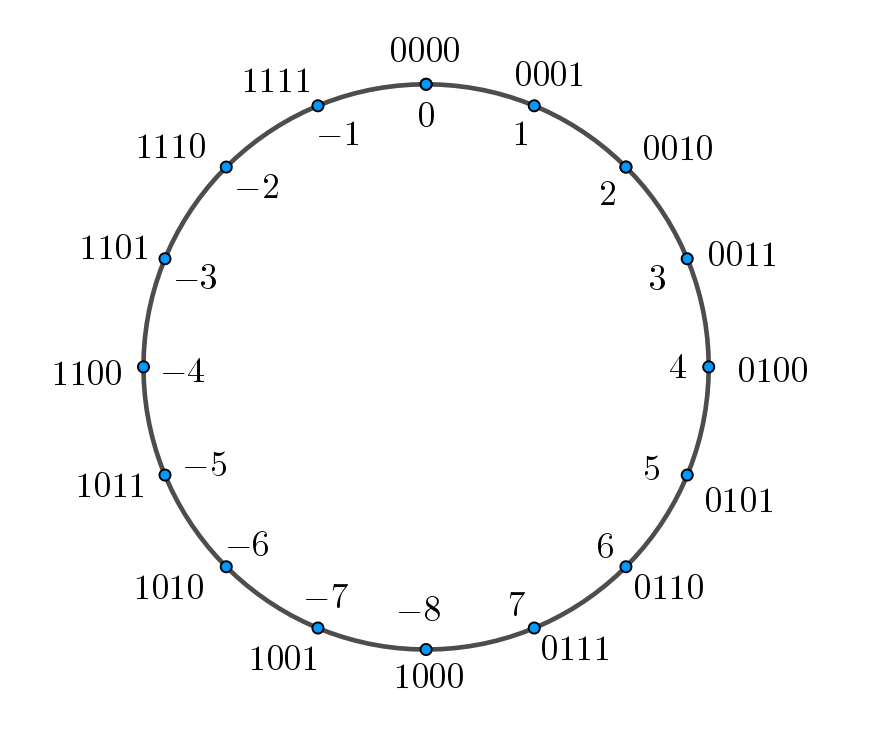
图2：补码在圆上的表示

按照上面数数的算法，我们知道 77 的后 99 位是 00，也就是 7+9=07+9=0 或者 −8+1=0-8+1=0，我们现在来分析这两个式子

先看后者，−8-8 在计算机中的表示为 11111111，11 的表示为 00010001，按理说 1111+0001=100001111+0001=10000，然而，现在我们只有四位二进制数，那么多出一位的 11 其实就是没有意义的，因此我们直接取后四位 00000000，也就是 00

再看前者，通过转化为二进制计算很容易得到这个结果（如下，取结果的后四位），但是这显然有点慢了

0111+100110000\begin{array}{ccccc} & 0 & 1 & 1 & 1\\ + & 1 & 0 & 0 & 1\\ \hline 1 & 0 & 0 & 0 & 0 \end{array}

换个想法，这个等式告诉我们在四位的二进制中 1616 会溢出为 00，现在想说明这件事情也不难，无论是从上文我们推导得出的，还是本节我们把数轴绕成圆（看成一个有 1616 格的时钟），都能知道这是一个模 24=162^4=16 的系统，因此只需要用 1616 除以 1616 取余数，就能得到 1616 在 00~77~−8-8~00 对应的次序，余 00 表示对应第一个数，即 00

下面来看一个计算溢出的示例

一个八位的的二进制数定义为 −257-257，那么其溢出后的值为多少？

  • 我们考虑用 −257-257 除以 28=2562^8=256，即商 −2-2，余 255255，对应在圆上从 00 开始计数 255255 次，最后得到的是 −1-1
  • 其实，如果把这个计算类比成上面钟表（此处为 256256 格）的计算，指针从 00 开始，往回（逆时针）走 257257 格，也就是先走 256256 格后回到 00，再往回走一格到 −1-1